Forasmuch as many have taken in hand to set forth in order a declaration of those things which are most surely believed among us, Even as they delivered them unto us, which from the beginning were eyewitnesses, and ministers of the word; It seemed good to me also, having had perfect understanding of all things from the very first, to write unto thee in order, most excellent Theophilus, That thou mightest know the certainty of those things, wherein thou hast been instructed.

Luke 1.1f

The correlation coefficient is a mathematical measure of the relation between two data sets. It is the standard measure used by scientist and statisticians throughout the world to determine if there is some common factor that causes two data sets to move together, rising and falling in a similiar fashion.

The coefficient ranges between the values of +1 and -1. The maximum value (+1) is attained when two sets of data rise and fall together by similiar amounts. The minimum value of -1 is attained when the two data sets move in opposite directions, one rising when the other falls. The value of zero indicates that the two data sets rise and fall independantly, that is, they are uncorrelated.

This is extremely significant for the study of the Wheel because it provides primary evidence of God's supernatural design of the Bible. Aspects of Scripture that are necessarily independent within a naturalistic world view, such as the structure of the Wheel or the correlation between the sixty-six chapters of Isaiah with the sixty-six books of the Bible, are found to be united by highly correlated word distributions. In some cases, the correlation coefficient attains values above 0.9, which is nothing less than absolute scientific proof of God's divine design of His Holy Word.

If you are unfamiliar with the idea of the correlation coefficient, I have prepared these four examples to show how it relates to various data sets.

These two data sets are highly correlated, which is visually apparent since they rise and fall together. The reason the coefficient is still somewhat less than unity (+1) is because there is not a perfect match in the relative magnitude of the variations.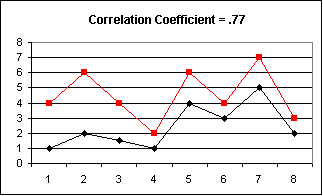
This graph shows how sensitive the correlation coefficient is to minor variations. It differs from the one above by only one data point: the fourth value in the black sequence was changed from 1 to 5, causing the graphs to cross (move in opposite directions). This caused the coefficient to drop from .77 to .18.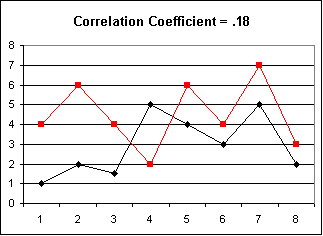
This graph shows what happens when we change just one more data point in the black sequence: the value of the sixth point was changed from 3 to 7. The graphs are now completely uncorrelated.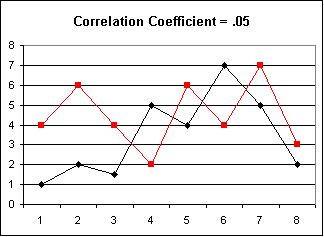
This graph shows what happens when the data sets move in opposite directions with similiar relative magnitudes, which results in a large negative value of the correlation coefficient.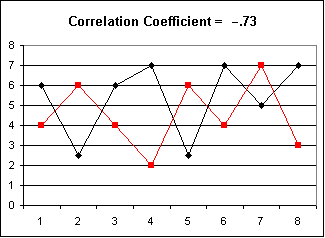

Questions? Comments? Join the discussion on the Bible Wheel Forum!