|
And for that the dream was doubled unto Pharaoh twice; it is because the thing is established by God,
and God will shortly bring it to pass.
Genesis 41:32
The term repdigit  denotes any integer that is
represented by single repeated digit, such as 11, 666, 777777, or 9999999. Any repdigit is a multiple of a repunit.
For example, the repdigit 999 is equal to 9 times the repunit 111. The repunits are
denoted by Rn, where n indicates the number of repeated units. For example: R3 = 111 and R4 = 1111.
Thus we write 999 = 9 x R3. When confusion is unlikely,
the multiplication sign can be dropped, and we will write 999 = 9R3. denotes any integer that is
represented by single repeated digit, such as 11, 666, 777777, or 9999999. Any repdigit is a multiple of a repunit.
For example, the repdigit 999 is equal to 9 times the repunit 111. The repunits are
denoted by Rn, where n indicates the number of repeated units. For example: R3 = 111 and R4 = 1111.
Thus we write 999 = 9 x R3. When confusion is unlikely,
the multiplication sign can be dropped, and we will write 999 = 9R3.
The value of a repunit depends on the base in which is it written because it is defined in terms of
its digits. For example, the number 7 in base 10 is a repunit in base 2, because it is represented by writing 111 in that base.
In general, repunits in base b are given by the following formula:
Rn = (bn - 1)/(b - 1)
For example, in base 10 we have b = 10 and R3 = 111:
R3 = (103 - 1)/(10 - 1) = 999/9 = 111

I became fascinated with repunits and repdigits after discovering that they are fundamentally related to the
Holographic Generating Set (GenSet for short) derived from the
alphanumeric integration of the introductory verses of Genesis and John (see
Creation Holograph). The GenSet is defined as the set
(A = 27, B = 37, C = 73). These three numbers are geometrically
related, consisting of the third Cube, 33 = 27, and
the fourth Hexagon/Star
pair 37/73. These number forms are closely related because Hexagons give the
differences between successive Cubes. For example:
43 - 33 = 64 - 27 = 37 = Hex(4)
When the GenSet is augmented to include the sum of its elements,
D = A + B + C = 137, we find the famous first aproximation to the
Fine Structure Constant which governs the
interaction of Light and Matter, a subject intimately related to the
creation passages in Genesis and John.
The Creation Holograph reveals an amazingly dense set of self-reflective
alphanumeric and geometric relations that can be expressed as simple combinations of
GenSet elements. Here are a few of the most obvious (recall Tri(n) denotes the nth
triangular number):
Genesis 1:1 = 100A + 1 = BC = Tri(C) = Tri(B) + 2AB = 100B - AB
Genesis 1:1 + AB = John 1:1 + C = AD + 1 = 100B
Genesis 1:1 + John 1:1 = AB + C2 = Tri(112)
The first line shows five independent representations of Genesis 1:1, with two of them
based on triangular forms of GenSet numbers, which are themselves geometric. Multiples of 10 and 100 appear frequently. Besides its integration
with the Creation Holograph (from which it was derived), the GenSet is also extremely self-reflective and
deeply integrated with base 10, as seen in this table of binary products:
| Selected Binary Products from Generating Set |
| BC |
37 x 73 |
2701 |
2700 + 1 |
A x 102 + 1 |
| AD |
27 x 137 |
3699 |
3700 - 1 |
B x 102 - 1 |
| AA |
27 x 27 |
729 |
730 - 1 |
C x 101 - 1 |
| BB |
37 x 37 |
1369 |
1370 - 1 |
D x 101 - 1 |
| CD |
73 x 137 |
10001 |
10000 + 1 |
....104 + 1 |
| AB |
27 x 37 |
999 |
1000 - 1 |
....103 - 1 |
The table shows the relation between all four elements of the GenSet with themselves and factors of 10, 100, 1000, and 10000 plus or minus one.
These identities, and many more, are discussed in the GenSet article. Of utmost significance is
its relation to the name of our Creator:
Jesus Christ = 2368 = AB + B2 = Cube(4) x Hex(4).
To see the connection between the GenSet and the repdigits, we begin by considering repdigits of the
form 9R2m. These repdigits can be algebraically factored as follows:
9R2m = 102m - 1 = (10m - 1)(10m + 1)
This is the standard formula for the difference of squares which can always be algebraically factored as
x2 - y2 = (x - y)(x + y).
This means that when n is even, the factors of 9Rn follow a symmetric pattern:
| 9R2 = |
99 = |
9 x 11 = |
(101 - 1)(101 + 1) |
| 9R4 = |
9999 = |
99 x 101 = |
(102 - 1)(102 + 1) |
| 9R6 = |
999999 = |
999 x 1001 = |
(103 - 1)(103 + 1) |
| 9R8 = |
99999999 = |
9999 x 10001 = |
(104 - 1)(104 + 1) |
The first thing to note is that 9R2m = 9Rm x (10m + 1).
For example, 9R6 = 9R3 x 1001. Thus, the even repdigits are just multiples of the odd repdigits.
This is a special case of the theorem
that says "If n is a multiple of m, then Rn is a multiple of Rm".
Using the mathematical notation of a vertical line to
signify the word "divides", this theorem is written "If m|n then Rm|Rn" and read as
"If m divides n, then Rm divides Rn."
The connection with the GenSet is now obvious. All four elements of the
augmented GenSet are found as paired factors of the repdigits 9R3 and 9R8:
| From 9R3: |
999 = 103 - 1 = 27 x 37 = AB |
| From 9R8: |
10001 = 104 + 1 = 73 x 137 = CD |
The pattern of powers of ten plus or minus one recalls what we saw in the table of binary products
above. This is the wonder of the GenSet. It was designed by God to lead us ever deeper into
His mathematical design of all creation. I originally derived it from the Creation Holograph.
I then discovered that
it could be defined from the continued fraction expansion
of the Fine Structure Constant (which itself forms a profound connection between Quantum Physics and the alphanumeric structure
of Scripture). And now I see that it relates to the repdigits.
Another link between the Repdigits and the Creation Holograph is found in the
prime number 271 which divides
R5 = 11111 = 41 x 271. Like the elements of the GenSet, this number is geometric. It is the
Tenth Centered Hexagon Number, 271 = Hex(10) = 103 - 93. It plays a very significant
role in the creation of light fragment of the Creation Holograph,
where it is symmetrically coordinated with
the Number 37 = B = Hex(4):

These symmetrically coordinated numbers from the Creation Holograph are also symmetrically coordinated factors in the
3rd and 5th repdigits:
| 9R3 |
= 999 |
= 27 x 37 = |
AB |
| 9R5 |
= 99999 |
= 271 x 369 = |
(10A + 1)(10B - 1) |
There are many repetitive patterns with variations on themes, such as the formal similarity to the factors of even
repunits R2m = (10m + 1)(10m - 1) and the binary products of GenSet elements.
Another variation is on the theme of "2 and 7" in the
numbers 27, 207, 271, 2701 which all play essential roles in the Creation Holograph.
And yet another fascinating variation is seen in the table of the GenSet reciprocals:
| Reciprocals of Generating Set Elements |
| 1/A = 1/27 = 0.037037037037 ... repeating digits of B |
| 1/B = 1/37 = 0.027027027027 ... repeating digits of A |
| 1/C = 1/73 = 0.01369863... repeating digits of 1369863 = 9999D and 1369 = B2 |
| 1/D = 1/137 = 0.00729927... repeating digits of 729927 = 9999C and 729 = A2 |
The digits in the GenSet reciprocals are multiples of the GenSet elements, just as we saw with their binary products.
The GenSet is profoundly self-reflective and integrated with the repdigits. It has unique properties found in no other set of
numbers, especially in light of their additional geometric nature.
It is truly amazing that this set was discovered through the
analysis of the intrinsic alaphanumeric structure of the creation passages of the Holy Bible. What a witness to the wisdom of our Creator
and Teacher!
So now the big question is this -
"What is the mathematical and symbolic significance of the repdigits?" The answer is no less astounding than
everything that led up to the question. As it turns out,
the repdigits are fundamental to the restoration of unity following the division
that was required for creation.
Repdigits, Creation, and the Restoration of Unity following Division
In the beginning God created the heaven and the earth.
And God said, Let there be light: and there was light.
And God saw the light, that it was good:
and God divided the light from the darkness.
Genesis 1:1-4
How does God create the universe? The Bible reveals that He created all things through His Word,
as it is written:
In the beginning was the Word, and the Word was with God, and the Word was God.
The same was in the beginning with God. All things were made by him; and without him was not any
thing made that was made. In him was life; and the life was the light of men.
And the light shineth in darkness; and the darkness comprehended it not.
John 1:1-5
The word translated as "Word" in John 1:1 is Logos.
This also is a title of the Second Person of the
Godhead, "whose name is called the Word of God" (Rev 19:13).
This is the deepest meaning of the Second Letter (Bet = House), which
simultaneously signifies the Son of God (Bet KeyWord Ben,
see Second Psalm) and the Word of God
(see Logos Holograph = Hebrews 4:12 and Bet = 412 = 2 x Word (Davar)).
All these ideas are ultimately subsumed under the Numerical Category
defined by the Number 2,
which contains all concepts relating to Division, Duality, Image, and Reflection.
Thus the Son (Ben) is the Second Person of the Trinity and the "image of the invisible God" (Col 1:15).
The Number 2 is one of the most obvious symbolic numbers in Scripture. Its meaning
can be traced very easily through the Second Day (Division of the Waters),
the Second Commandment (No graven images),
the Second Seal (Great Sword = Instrument of Division).
Ultimately, it is based on the meaning of the name of the Second Letter
(Bet = House) as that which divides between what is "in" and what is "out" and this is basis of the very concept of
"definition" and so lies at the root of the meaning of "the Word"
that divides between what "is" an "is not" - the
very Sword of the Spirit by which God created all that is (Ephesians 6:17). This is the "sharp two-edge sword"
emerging from the mouth of our Creator, the Lord Jesus Christ (Rev 1:16). Thus we see that the biblical revelation of
how God created, including the essence of the concept of "word" itself, is based on the nature of the Triune Godhead
and embedded in the symbolic strucutre of the Hebrew alphabet!
Endless glory! The Christian revelation is the true revelation of Ultimate Reality!
This is explained in great detail in the Synopsis of Spoke 2 in the Bible Wheel book.
The manifold connections between the Number 2 and the concepts of
Division, Word, and the process of Creation form a very
dense symbolic matrix that unites the Bible Wheel, Biblical Holographs, and Trinitarian Theology. The intuition that there also was
some deep connection with the repdigits has been floating in the back of my mind for many years now. The full understanding
finally emerged when I looked closely at what happens when unity is divided.
Consider what happens when we divide unity by seven:
1/7 = 0.142857 142857 142857 142857 142857 ...
The repeating sequence of digits - 142857 - is called the repetend,
which I separated with spaces for clarity. All such repetends
are factors of the repdigits because the fraction must be returned to unity when multiplied by
its divisor:
1 = 7 x (1/7) = 7 x 0.142857 142857 142857... = 0.999999 999999 999999 ...
Many folks are surprised when they first learn that an infinite sequence of nines following
the decimal point is exactly equal to unity. But a little reflection on what happens when we divide and multiply
should make it clear. Consider 1/3 = 0.333333.... When we multiply by 3 we must arrive at 1 = 3 x (1/3) = .999999....
This is why the repetends are always factors of the redigits:
7 x 142857 = 999999 = 106 - 1 = 9R6
Note that all the numbers in this equation are integers, and that the divisor is related to the
exponent of the number 10: 6 = 7 - 1.
The number 7 is called a Full Repetend Prime  in base 10 because its repetend consists of six digits, the maximum possible for the number 7. This maximum is found
using Fermat's Little Theorem
in base 10 because its repetend consists of six digits, the maximum possible for the number 7. This maximum is found
using Fermat's Little Theorem  : :
ap-1 = 1 mod p if p does not divide a.
This theorem shows that p will always divide 10p-1 - 1 = 9Rp-1 for all primes p other than
2 or 5 which are excluded because they divide 10. Fermat's Little theorem gives the largest possible
value of a period length for a prime. The exact value is given
by Euler's Totient Function  , phi(p).
Here is a table of the first four Full Repetend Primes that shows how they relate to the repdigits: , phi(p).
Here is a table of the first four Full Repetend Primes that shows how they relate to the repdigits:
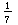 = = 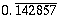 | 7 x 142857 = 9R6 |
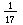 = = 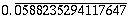 | 17 x 588235294117647 = 9R16 |
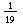 = =  | 19 x 52631578947368421 = 9R18 |
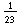 = = 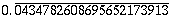 | 23 x 434782608695652173913 = 9R22 |
 1 x 142857 = 142857
1 x 142857 = 142857
3 x 142857 = 428571
2 x 142857 = 285714
6 x 142857 = 857142
4 x 142857 = 571428
5 x 142857 = 714285
|
| 1 + 6 = 7 | | 1 + 8 | = 9 |
| 3 + 4 = 7 | | 4 + 5 | = 9 |
| 2 + 2 = 7 | | 2 + 7 | = 9 |
|
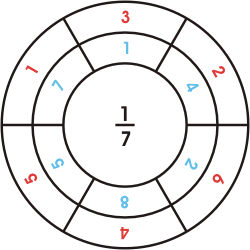
The Full Repetend Primes generate the cyclic numbers  which
got there name from the fact that their digits cycle through the various possible positions while remaining in the
same order. The first digit moves to the last position, the second to the first, and so on, as shown for the
cyclic number generated by the reciprocal of seven. I have shown the long division on the right using
blue for the sequence of quotients and red for the sequence of remainders. The facinating thing about
cyclic numbers is that the sequence of remainders 1 3 2 6 4 5 gives the
sequence of multiples that shift the digits one space over. The circle is a convenient way to display
patterns found in the repeating digits. The inner circle shows the quotient in blue, and the
outer circle shows the remainder in red. The circles have interesting patterns and symmetry. Starting
at the top of the inner circle and reading clockwise, we find the digits of the repetend, 142857. Starting once
space back from the top of the outer circle gives the sequence of remainders.
Remainders (red) that lie on opposite sides of the circle always add to the value of the divisor (7), and
quotients (blue) that lie on opposite sides always and to one less than the base (9), which is the digit
needed to return to unity.
To find where the sequence starts for a given multiple, look for the corresponding remainder and begin with
the blue digits one space clockwise. For example, to find the sequence for 6 x 142857, start with blue eight on the
inner circle clockwise from the red 6 on the outer circle and read clockwise to get 857142. which
got there name from the fact that their digits cycle through the various possible positions while remaining in the
same order. The first digit moves to the last position, the second to the first, and so on, as shown for the
cyclic number generated by the reciprocal of seven. I have shown the long division on the right using
blue for the sequence of quotients and red for the sequence of remainders. The facinating thing about
cyclic numbers is that the sequence of remainders 1 3 2 6 4 5 gives the
sequence of multiples that shift the digits one space over. The circle is a convenient way to display
patterns found in the repeating digits. The inner circle shows the quotient in blue, and the
outer circle shows the remainder in red. The circles have interesting patterns and symmetry. Starting
at the top of the inner circle and reading clockwise, we find the digits of the repetend, 142857. Starting once
space back from the top of the outer circle gives the sequence of remainders.
Remainders (red) that lie on opposite sides of the circle always add to the value of the divisor (7), and
quotients (blue) that lie on opposite sides always and to one less than the base (9), which is the digit
needed to return to unity.
To find where the sequence starts for a given multiple, look for the corresponding remainder and begin with
the blue digits one space clockwise. For example, to find the sequence for 6 x 142857, start with blue eight on the
inner circle clockwise from the red 6 on the outer circle and read clockwise to get 857142.
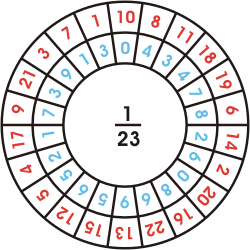
Wheel of 22 Spokes generated
by the Number 23 = Aleph + Tav |
Number 23, the fourth Full Repetend Prime, generates a wheel of 22 Spokes just like the Bible Wheel.
The same patterns of opposite remainders (red) adding to the divisor (23)
and opposite quotients adding to 9 is valid for all Full Repetend Primes.
Not all primes are Full Repetend Primes. The sequence begins 7, 17, 19, 23, and may
be viewed here  .
I find it intriguing that the Bible Wheel corresponds to the cycle of length 22 generated by the fourth Full Repetend Prime, the
Number 23, which is the ordinal value of Aleph (1) + Tav (22), adn that these letters combine to
seal the Wheel
with the word .
I find it intriguing that the Bible Wheel corresponds to the cycle of length 22 generated by the fourth Full Repetend Prime, the
Number 23, which is the ordinal value of Aleph (1) + Tav (22), adn that these letters combine to
seal the Wheel
with the word 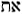 (ot) meaning divine sign, miracle,
proof, or signature. My intuition now is leading me to think there is a
fundamental link that extends form the Creation Holograph and the GenSet through the Repdigits and Cyclic Numbers
all the way to the large-scale structure of God's Word in the
form of the Wheel. Facinating stuff! There are many other patterns of repdigits and repunits that I would like to share, but
they will have to wait for future articles. The essential insight I hope to get across in this article is this: (ot) meaning divine sign, miracle,
proof, or signature. My intuition now is leading me to think there is a
fundamental link that extends form the Creation Holograph and the GenSet through the Repdigits and Cyclic Numbers
all the way to the large-scale structure of God's Word in the
form of the Wheel. Facinating stuff! There are many other patterns of repdigits and repunits that I would like to share, but
they will have to wait for future articles. The essential insight I hope to get across in this article is this:
- God created all that is with His Word.
- God's Word creates through symbolic Division.
- The symbolic Division related to Creation is mathematically restored to Unity through the Repdigits.
- The Repdigits are fundamentally integrated with the GenSet.
- The GenSet is the mathematical basis of the Creation Holograph which unites the fundamental creation passages found in
the first chapters of Genesis and John.
In essence, the repdigits are required to "zip up" the numbers after they have been divided. They are fundamental to
both mathematics and the alphanumeric structure of the Creation Holograph.
A new Repunit Theorem
I was reading a message  on the Fivedoves site
by Ian Mallet who noted an interesting property of the Number 37. Here is how he explained it: on the Fivedoves site
by Ian Mallet who noted an interesting property of the Number 37. Here is how he explained it:
Some years ago, I made
an amazing discovery concerning the number 37,
the key number of Genesis 1:1 and of the names of Jesus Christ. I found that any multiple of
37 can be split into two separate numbers and then
if each new number is cubed and both results are added together, the result is
still a multiple of 37. For example,
let's look at the number 37 itself: The
number 37 splits into 3 and 7. Cubing the
figure 3 (3 x 3 x 3) results in 27 and cubing the figure 7 (7 x 7 x 7) results
in 343. The sum of 27 + 343 is 370 or 10 x 37. This works for all numbers having a factor of
37.
Ian's discovery intrigued me, so I wrote a quick little bit of computer code to test his assertion.
And while I was at it, I thought I would see if the same pattern would work with other numbers and other powers.
The results were quite surprising. I found that the same pattern worked for all multiples of 41 with the 5th power,
and all multiples of 53 with the 13th power. Since I had been meditating on repdigits for a number of years,
I immediately recognized these numbers as
prime factors of repunits  with the power
corresponding to the length of the repunit: with the power
corresponding to the length of the repunit:
R3 = 111 = 37 x 3
R5 = 11111 = 41 x 271
R13 = 1111111111111 = 53 x 20964360587
The hypothesis then states that:
37 divides R3 so 37 also divides 33 + 73 = 370 = 37 x 10
41 divides R5 so 41 also divides 45 + 15 = 1025 = 41 x 25
53 divides R13 so 53 also divides 513 + 313 = 1222297448 = 53 x 23062216
I tested my hypothesis with the free online GMP software  that computes number theoretic
functions for integers of arbitrary length.
The hypothesis tested true for any multiples of repunit divisors, such as 6519 = 123 x 53.
Here are the three possible splits: that computes number theoretic
functions for integers of arbitrary length.
The hypothesis tested true for any multiples of repunit divisors, such as 6519 = 123 x 53.
Here are the three possible splits:
| 613 + 51913 = | 53 x 3740242686654128652727975169311275 |
| 6513 + 1913 = | 53 x 6975860965185939625428 |
| 65113 + 913 = | 53 x 71166725190969215362417677468826260 |
Alternately, we could use the fact that 123 is a multiple of 41 which divides
R5 and test the hypothesis for that pair:
| 65 + 5195 = | 41 x 918444531375 |
| 655 + 195 = | 41 x 28360164 |
| 6515 + 95 = | 41 x 2851813275300 |
A similar pattern works for repunits with an even number of digits, the only difference being that we
need to subtract rather than add the exponentiated parts.
For example, 137 divides R8.
Here are the three ways to split its multiple 3699 = 27 x 137:
| 38 - 6998 = | -137 x 416003360415093472320 |
| 368 - 998 = | -137 x 67333035287385 |
| 3698 - 98 = | 137 x 2508940500319632960 |
I continued testing the hypothesis with very large numbers and found it always worked.
I shared my idea with a friend Bruno Curfs, and he noted that we could attain a very simple proof
if we wrote the number to be split in the form y = a10k + b.
Theorem: Suppose d divides Rn. Let y = md be any multiple of d.
Write y = a10k + b, with 0 < k < log10(y).
For example, if y = 2368, and k = 2, then a = 23 and b= 68.
The theorem asserts: an - (-b)n = 0 mod d.
Proof:
From the definition of y we have: (y - b)n = an10nk mod d.
Now by assumption, d divides Rn = (10n - 1)/9 so 10n = 1 mod d.
Therefore an10nk = an mod d and we have (y - b)n = an mod d.
Using the Binomial Theorem  we find (y - b)n = yP(y,b) + (-b)n where P(y,b) is an integer polynomial
made up of Binomial Coefficients and powers of y and b.
we find (y - b)n = yP(y,b) + (-b)n where P(y,b) is an integer polynomial
made up of Binomial Coefficients and powers of y and b.
Therefore an = (y - b)n = yP(y,b) + (-b)n = (-b)n mod d, and we have the result desired.
QED
This proof can be easily extended to any base. I am not certain if this is a new theorem. It could exist somewhere in the
vast realm of mathematical literature, but if so, I have never seen it. In any case, it shows how the study of the alphanumeric
structure of Scripture can lead to new mathematical insights. Praise God, our Guide and Teacher!
| 
